js - 深拷贝非递归实现

深度优先 DFS

对于二叉树的深度优先算法，遍历顺序如下图所示：

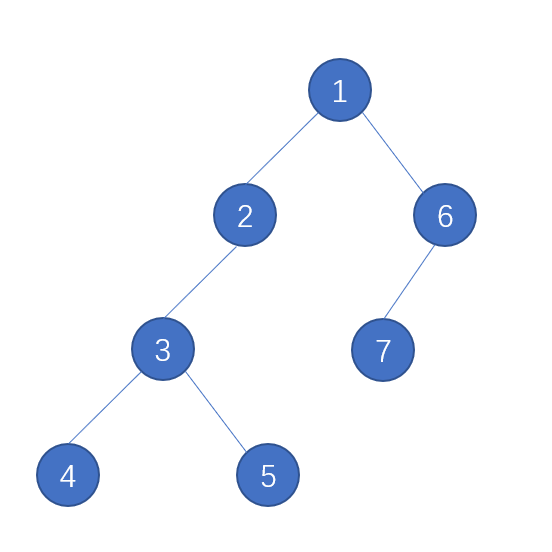
对应递归版本的代码实现如下：

function dfs(root) {
  visit(root)
  if (root.left) {
    dfs(root.left)
  }
  if (root.right) {
    dfs(root.right)
  }
}

对于非递归版本而言，我们需要借助栈来实现：

function dfsNonRecursive(root) {
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    visit(node)
    if (node.right) {
      stack.push(node.right)
    }
    if (node.left) {
      stack.push(node.left)
    }
  }
}

注意：这里需要先将右结点推入栈中，再将左节点推入栈中，这与栈的工作原理有关，也就是先进后出。

了解了深度遍历的原理后，我们就可以开始写我们的深拷贝代码了。 由于 JavaScript 中的对象子节点可能不只有一个，所以我们需要 将所有的子节点推入到栈中，而且同上面二叉树的深度遍历类似，我们 需要先将右结点推入栈中。

参考下面的例子：

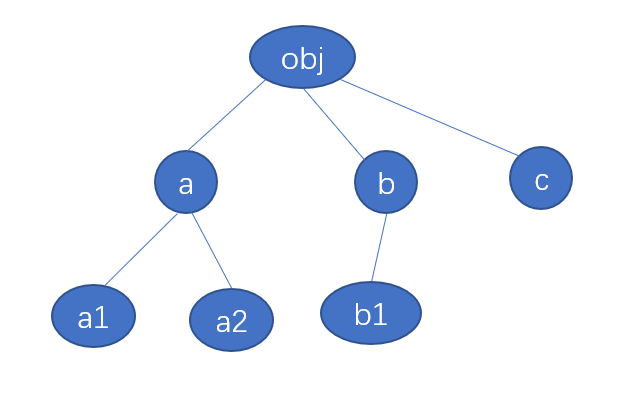
我们要推入栈的顺序如下：

当 a 出栈时，由于 obj.a 为引用类型，根据深度优先算法， 我们需要将 a 的子节点也推入栈中：

注意：还是需要先将右结点推入到栈中。

为了方便操作，我们用 src[key] 保持当前要拷贝的对象，具体代码如下：

function isObject(obj) {
  return typeof obj === 'object' && obj !== null
}

/**
 * 深度优先非递归实现
 * 这里只针对 Array 和 Object 的拷贝
 * @param {*} obj
 */
export function deepCopyDFS(obj) {
  // 对于非对象类型，直接返回
  if (!isObject(obj)) {
    return obj
  }

  // Map<src, dest>:为了避免循环引用
  const seen = new Map()
  seen.set(obj, obj)
  const result = Array.isArray(obj) ? [] : {}
  const stack = [[obj, result, null]]

  // 以上面的对象为了： obj = {a: {a1: 1, a2: 2}, b: 1, c: {c1: 1}}
  while (stack.length) {
    const [src, dest, key] = stack.pop()
    // 相当于遍历根结点： 此时栈中的数据为
    //          top
    // |                       |
    // |                       |
    // |   [src, dest, 'a']       |
    // |   [src, dest, 'b']       |
    // |   [src, dest, 'c']       |
    // ------------------------
    if (key === null) {
      const keys = Object.keys(src)
      for (let i = keys.length - 1; i >= 0; i--) {
        stack.push([src, dest, keys[i]])
      }

      // 对于 key 的判断，例如：obj.a
    } else if (isObject(src[key])) {
      // 需要判断是否已经遍历过，避免循环引用
      if (seen.has(src[key])) {
        dest[key] = seen.get(src[key])
      } else {
        // 对于引用类型，再次将子节点推入栈中
        dest[key] = Array.isArray(src[key]) ? [] : {}
        stack.push([src[key], dest[key], null])
      }
    } else {
      // 对于基本数据类型，直接添加即可
      dest[key] = src[key]
    }
  }
  return result
}

需要注意的是，将所有的子节点推入到栈中对应的代码为 for (let i = keys.length - 1; i >= 0; i--) {}。

广度优先 BFS

广度优先算法其实和深度优先算法类似，只不过我们采用的队列去实现，而不是栈。 同时，子节点入队的顺序也将改为从左结点开始。对应代码如下，注意高亮部分：

export function deepCopyBFS(obj) {
  if (typeof obj !== 'object' || obj === null) {
    return obj
  }
  const result = Array.isArray(obj) ? [] : {}
  const queue = [[obj, result, null]]
  const seen = new Map()
  seen.set(obj, obj)
  while (queue.length) {
    const [src, dest, key] = queue.shift()
    if (key === null) {
      Object.keys(src).forEach(key => {
        queue.push([src, dest, key])
      })
    } else if (isObject(src[key])) {
      if (seen.has(src[key])) {
        dest[key] = seen.get(src[key])
      } else {
        dest[key] = Array.isArray(src[key]) ? [] : {}
        queue.push([src[key], dest[key], null])
      }
    } else {
      dest[key] = src[key]
    }
  }
  return result
}

测试

import { deepCopyBFS, deepCopyDFS } from '.'
describe('deepCopy', () => {
  let keys = []
  const a = new Proxy(
    { a1: 1, a2: 2 },
    {
      get(target, key) {
        if (!keys.includes(key)) keys.push(key)
        return Reflect.get(target, key)
      },
    },
  )
  const b = 1
  const c = new Proxy(
    { c1: 1 },
    {
      get(target, key) {
        if (!keys.includes(key)) keys.push(key)
        return Reflect.get(target, key)
      },
    },
  )
  const proxy = new Proxy(
    { a, b, c },
    {
      get(target, key) {
        if (!keys.includes(key)) keys.push(key)
        return Reflect.get(target, key)
      },
    },
  )

  beforeEach(() => {
    keys = []
  })

  describe('DFS non-recursive implementation', () => {
    it('should perform the correct deepCopy function', () => {
      // TODO: add test
      expect(deepCopyDFS(null)).toEqual(null)
      function func() {}
      expect(deepCopyDFS(func)).toEqual(func)
      expect(deepCopyDFS([1, 2, 3, { a: 1 }])).toEqual([1, 2, 3, { a: 1 }])
      const obj1 = { a: 1, b: 1, c: [1, 2] }
      const copiedObj1 = deepCopyDFS(obj1)
      expect(copiedObj1).toEqual(obj1)
      copiedObj1.c.push(3)
      expect(copiedObj1).not.toEqual(obj1)
    })

    it('should avoid cycle reference', () => {
      const obj1 = { name: 'obj1' }
      const obj2 = { name: 'obj2' }
      // obj1.a = obj2,  obj2.a = obj1
      // cycle reference
      obj1.a = obj2
      obj2.a = obj1
      const copiedObj1 = deepCopyDFS(obj1)
      expect(copiedObj1).toEqual(obj1)
    })

    it('should perform DFS copy', () => {
      deepCopyDFS(proxy)
      expect(keys).toEqual(['a', 'a1', 'a2', 'b', 'c', 'c1'])
    })
  })

  describe('BFS non-recursive implementation', () => {
    it('should perform the correct deepCopy function', () => {
      // TODO: add test
      expect(deepCopyBFS(null)).toEqual(null)
      function func() {}
      expect(deepCopyBFS(func)).toEqual(func)
      expect(deepCopyBFS([1, 2, 3, { a: 1 }])).toEqual([1, 2, 3, { a: 1 }])
      const obj1 = { a: 1, b: 1, c: [1, 2] }
      const copiedObj1 = deepCopyBFS(obj1)
      expect(copiedObj1).toEqual(obj1)
      copiedObj1.c.push(3)
      expect(copiedObj1).not.toEqual(obj1)
    })

    it('should avoid cycle reference', () => {
      const obj1 = { name: 'obj1' }
      const obj2 = { name: 'obj2' }
      // obj1.a = obj2,  obj2.a = obj1
      // cycle reference
      obj1.a = obj2
      obj2.a = obj1
      const copiedObj1 = deepCopyBFS(obj1)
      expect(copiedObj1).toEqual(obj1)
    })

    it('should perform DFS copy', () => {
      deepCopyBFS(proxy)
      expect(keys).toEqual(['a', 'b', 'c', 'a1', 'a2', 'c1'])
    })
  })
})